A fast implementation of aLRT in PhyML.
Implemented by Jean-François Dufayard from original PhyML, based on Anisimova and Gascuel (2006) paper.
Please cite:
"Approximate likelihood ratio test for branchs: A fast, accurate and powerful alternative."
"Approximate likelihood ratio test for branchs: A fast, accurate and powerful alternative."
Anisimova M., Gascuel O.
Systematic Biology, 55(4), 539-552, 2006.
Content
Here you can find a beta-version of binaries that implement the algorithm described in our Syst. Biol. paper. Feedback and comments are much welcome.This PhyML version contains two main improvements:
- the aLRT for branches, which is much faster than bootstrap, but not equivalent (see below).
- some new optimization procedures based on careful inspection of NNIs.
Usage
PhyML-aLRT uses the same arguments as the original PHYML. Five branch supports are available:- Felsenstein’s bootstrap,
- aLRT statistics,
- aLRT parametric (Chi2-based, see our Syst. Biol. paper) branch support,
- aLRT non-parametric branch support based on a Shimodaira-Hasegawa-like procedure (not described in our Syst. Biol. paper),
- and a combination of these two latters supports, that is, the minimum value of both.
Download
Binaries for various platforms are available here.From Felsenstein’s bootstrap to aLRT
Both approaches are clearly different, as detailed in our Syst. Biol. paper, and we encourage any user to read this paper for better understanding of the differences. Basically:- aLRT is much faster than bootstrap, as PhyML is run just once, while bootstraps requires running PhyML 100 to 1000 times.
- the bootstrap proportion is a repeatability measure; when the bootstrap proportion of a given clade is high, one can be quite confident that this clade would be inferred again if another original data sample was available and analyzed by the same tree-building method (which does not mean that the clade is true).
-
aLRT assesses that the branch being studied provides a significant likelihood gain, in comparison with the null hypothesis that involves collapsing that branch but leaving the rest of the tree topology identical. In our Syst. Biol. paper we interpreted the aLRT statistics using the standard null-distribution, which is based on a mixture of Chi2s. It appeared that with real data, the resulting test tends to be liberal due to violations of the parametric assumptions. In that respect, aLRT parametric interpretation seems to be close to Bayesian posteriors. We then implemented a Shimodaira-Hasegawa-like procedure, which is non-parametric, much less liberal, and seems to behave well (see graphics below). Moreover, we provide the user with an even more conservative option, that is, the minimum of Chi2-based and SH-like supports (in some rare cases SH-like support is below Chi2-based one, see Deficiens mARN dataset below).
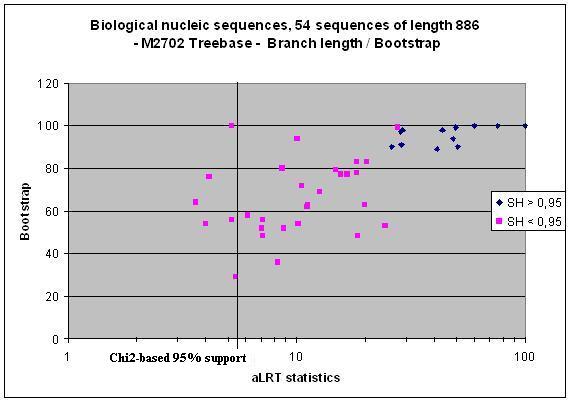
Another exemple from the Deficiens mARN family.
More graphics, from Treebase datasets: Matrix 2576; Matrix 2733; Matrix 2804.
Test dataset
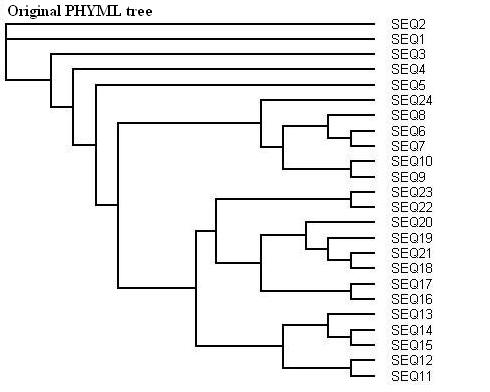
Here is a protein dataset (C8 alpha chain precursor) that can be used with aLRT-PhyML for test purpose. The resulting trees that are obtained with three support options are shown below. To get those trees in Newick format, click on figures. This example shows that bootstrap proportions and aLRT SH-like supports basically agree, while Chi2-based supports tend to be more liberal. We also display the tree computed by the original PhyML, which has a loglikelihood 4.1 points below that of the new version.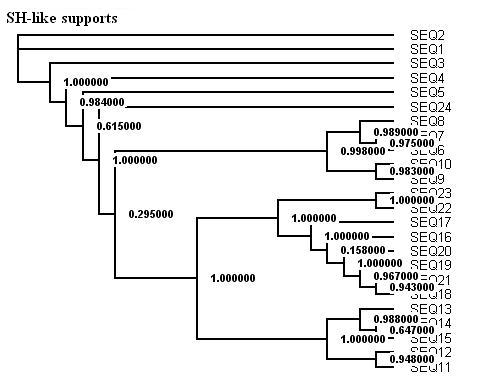
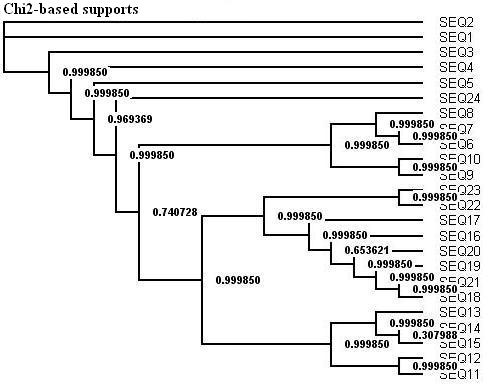
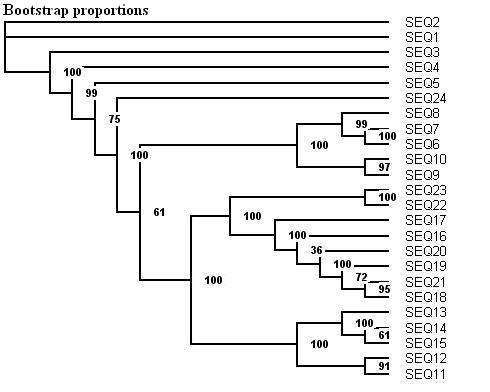
Contacts
For any questions about the algorithm, the options of the program or the source code, you can contact:- Maria Anisimova (author).
- Olivier Gascuel (author) LIRMM, Montpellier, France
- Jean-François Dufayard (programmer) LIRMM, Montpellier, France



